구조해석 및 유한요소법

1) 구조해석
기계요소나 기계요소들을 조합한 기계 등의 구조물이 외력을 받았을 때, 구조물의 강성, 응력분포, 변형량이 어떻게 되는가에 관해서 수치계산을 하여 그 근삿값을 알아내는 것이다.
구조해석은 탄성영역에서의 선형해석과 소성영역에서의 비선형해석으로 대별된다. 수치계산 방법으로는 일반적으로 유한요소법(FEM)을 쓰는 경우가 많다. 최근에는 컴퓨터의 발달에 의하여 퍼스널 컴퓨터로도 용이하게 구조해석을 할 수 있는 범용구조해석 소프트웨어를 이용해서 구조해석을 한다.
2) 유한요소법(FEM)복잡한 구조체를 삼각형이면 삼각형, 사각형이면 사각형등 간단한 기하학적 모양을 가지는 수많은 작은 단위구조로 나눌 수 있습니다. 이 단위구조를 유한요소(finite element)라고 하는데, 이 단위구조의 기하학적 모양이 단순하므로, 전체 구조에 대해서 이 단위구조에 작용하는 역학적 반응치들(각 절점당 3개의 변위치와 3개의 변위각, 그리고 3개의 반력과 3개의 모멘트)을 의외로 쉽게 구할 수 있습니다. 이렇게 각각의 단위구조에 대해서 구한 역학적 반응치들을 전체 시스템에서 합하여 복잡한 형태의 전체구조의 전체적 역학적 반응치를 구하는 기법을 유한요소법이라고 합니다.3) 매트릭스 구조해석
2차원 frame 구조를 해석하면서 보다 간편하게 과정을 가져가고자 고안된 기법입니다. 2차원 frame의 경우, 각 요소가 보요소(beam)로 간주됩니다. 이렇게 되면 각 요소의 끝 다른 요소와 만나는 점(이것을 절점, joint라고 합니다)에서의 반력이 모멘트와 전단력이 되고, 변형은 수직변위와 연직변위 그리고 회전각이 됩니다. 이 반력과 변형간의 관계가 각 요소마다 구해질 수 있고, 이것이 전체적인 시스템에서 합해지는데, 이 합해져서 전체적인 시스템에서의 역학적 반응치를 구하는 과정에 매트릭스 연산을 도입해서 보다 능률적으로 가져간 기법입니다.4) 유한요소법과 매트릭스 구조해석의 차이점
매트릭스 구조해석이나 유한요소법이나, 그 풀이과정에서 다차원 연립방정식이 도출되어, 이 해를 매트릭스 연산으로 풀어내는 것은 같습니다. 하지만 매트릭스구조해석이 2차원 frame을 대상으로 하는 방법이므로, 수계산 수준으로 가능한 반면, 유한요소밥은 주로 2, 3차원 solid 구조를 대상으로 하므로, 미지수가 많고, 연립방정식 숫자가 워낙 많으므로 컴퓨터를 이용해서만 가능하다는 차이점이 있습니다.
 

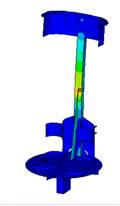
<적용 사례>